[Quick Pitch] On Extending Direct Preference Optimization to Accommodate Ties @NeurIPS 2025

Direct Preference Optimization (DPO) trains language models on pairs of preferred and dispreferred responses, \(y_w \succ y_l\). But not all pairs have a clear winner. For pairs without clear preference - i.e., ties - a common approach is to simply discard them (e.g., Llama3 and Qwen2). In this work, we are motivated by what Rao and Kupper observed 58 years ago:

"Any model which does not allow for the possibility of ties is not making full use of the information contained in the no-preference class."
A Generalization of the Bradley-Terry Model, Rao and Kupper, 1967

Our work introduce DPO variants that explicitly model the possibility of ties. This is done by replacing the Bradley-Terry model with two tie-compatible variants: the Rao-Kupper and the Davidson model. We then study the effect of including tied pairs in training on machine translation, summarization, and mathematical reasoning. Overall, we find that ties introduce a strong regularization effect to training (as measured by KL divergence), and that they could improve overall performance in many cases. If this interests you, read on!

DPO does not accommodate Ties

The Bradley-Terry model assigns probability that an item \(y_i\) will be preferred to item \(y_j\) in terms of their "strength" difference, \(d_{ij}=r_i-r_j\), where \(e^{r_i}\) is the "strength" of item \(y_i\). That is:

$$p^{BT}(y_i\succ y_j)=\frac{e^{r_i}}{e^{r_i}+e^{r_j}}=\sigma(r_i-r_j)$$

DPO uses policy-reference log-likelihood ratio \(\beta\log\frac{\pi_\theta(y_i|x)}{\pi_{ref}(y_i|x)}\) as the reward \(r_i\) and maximizes the log-likelihood of \(\log p^{BT}(y_i\succ y_j)\) over all pairs in a pairwise dataset. Because of this formulation, DPO does not allow tied pairs \(y_i \sim y_j\) in its dataset - it would be wrong to optimize \(\log p^{BT}(y_i\succ y_j)\) on ties!

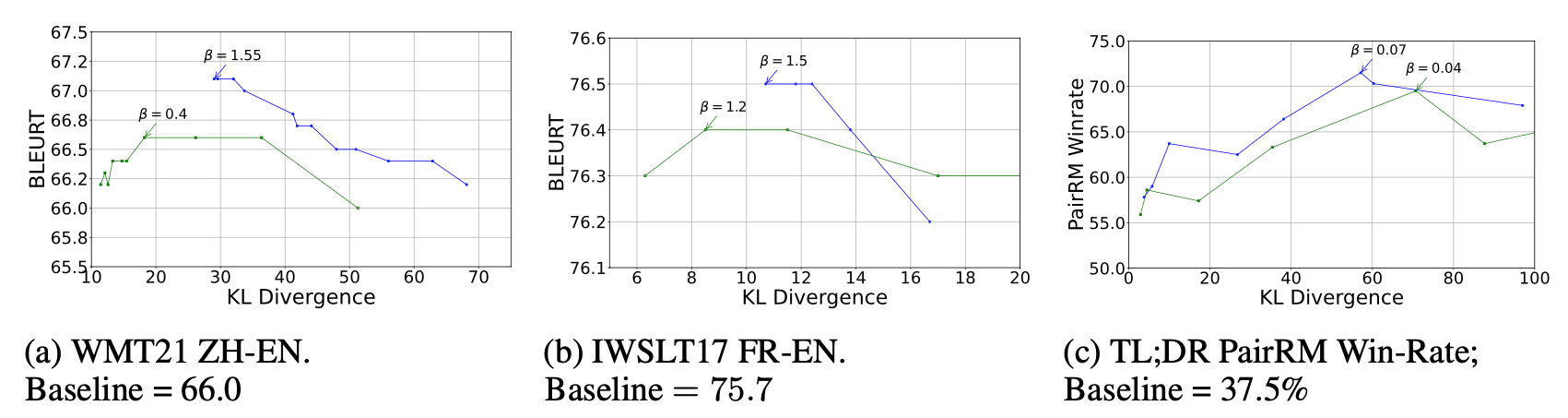
And indeed, including pairs that are actually ties to DPO training hurts performance. In the Performance versus KL divergence graphs below, the blue curve shows DPO systems trained on Clear Preference pairs (CP) and the green curve shows DPO systems trained on CP and Tied Pairs (TP). These operating curves are produced by training with different beta values. We find that adding TP to DPO training seems to incur a shift "down-and-to-the-left". That is, tied pairs hurts performance, but strengthen regularization.

Variants of Bradley-Terry that models Ties

To properly accommodate ties, we require alternative comparison models that assign probabilities to the event of ties. Luckily, there are two established Bradley-Terry variants that do this: the Rao-Kupper model and the Davidson model. These models assign both win and tie probabilities.

The Rao-Kupper model can be understood as Bradley-Terry with a margin \(\nu_{RK}\). Items with strengths close to each other is more likely to tie with each other:

$$P^{RK}(y_i\succ y_j)=\frac{\lambda_i}{\lambda_i + \nu_{RK}\lambda_j} = \sigma(d_{ij} - \log\nu_{RK})$$

$$P^{RK}(y_i\sim y_j)=\frac{(\nu_{RK}^2-1)\lambda_i\lambda_j}{(\lambda_i + \nu_{RK}\lambda_j)(\lambda_j + \nu_{RK}\lambda_j)} = (\nu_{RK}^2-1)\sigma(-d_{ij}-\log\nu_{RK})P^{RK}(y_i\succ y_j)$$

The Davidson model starts from Luce's choice theorem which states that a complete system of choice probability should satisfy \(P(y_i\succ y_j)/P(y_j \succ y_i)=\lambda_i / \lambda_j\) That is, comparison outcome should be based on the strength ratio of the items being compared only:

$$P^{D}(y_i\succ y_j)=\frac{\lambda_i}{\lambda_i + \lambda_j + \nu_{D}\sqrt{\lambda_i\lambda_j}} = \frac{1}{1+\exp(-d_{ij})+2\nu_D\exp(-d_{ij}/2)}$$

$$P^{D}(y_i\sim y_j)= 2\nu_D\exp(-d_{ij}/2)P^D(y_w\succ y_l)$$

In both models, the extra hyper-parameter \(\nu_{RK}\) and \(\nu_D\) control probability of a tie when two items have identical strength: the higher, the more likely a tie.

We then replace Bradley-Terry with these tie-compatible models and derive variants of DPO, DPO-RK and DPO-D, that maximize:

$$\log P(y_i\succ y_j)\text{ on Clear Preference; } \log P(y_i \sim y_j)\text{ on Tied Pairs}$$

In plain words, with DPO-RK and DPO-D, the dataset admits both tied pairs and clear preferences!

Benefits of Incoporating Ties

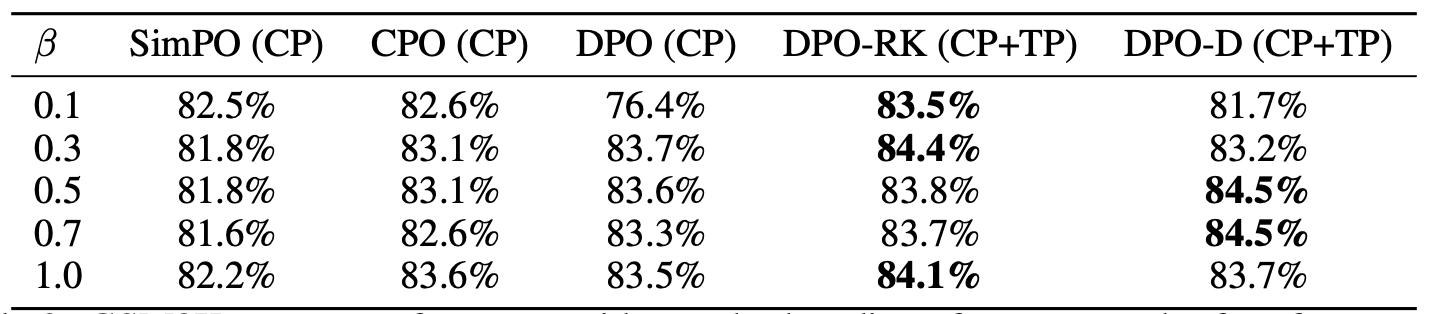
We experiment on Machine Translation, Summarization, and Mathematical Reasoning with several ways to label tied pairs automatically. We mainly compare systems trained with DPO-RK and DPO-D on both clear preferences and tied pairs (which we refer to as "DPO-RK(CP+TP)" and "DPO-D(CP+TP)") and those trained with DPO on Clear Preference only ("DPO(CP)").

Here are our findings on when and how can ties be useful:

• Tied Pairs = similarly scored responses. DPO-RK(CP+TP) and DPO-D(CP+TP) produce similarly-performing systems as DPO(CP), but at much smaller KL divergence relative to the reference model.

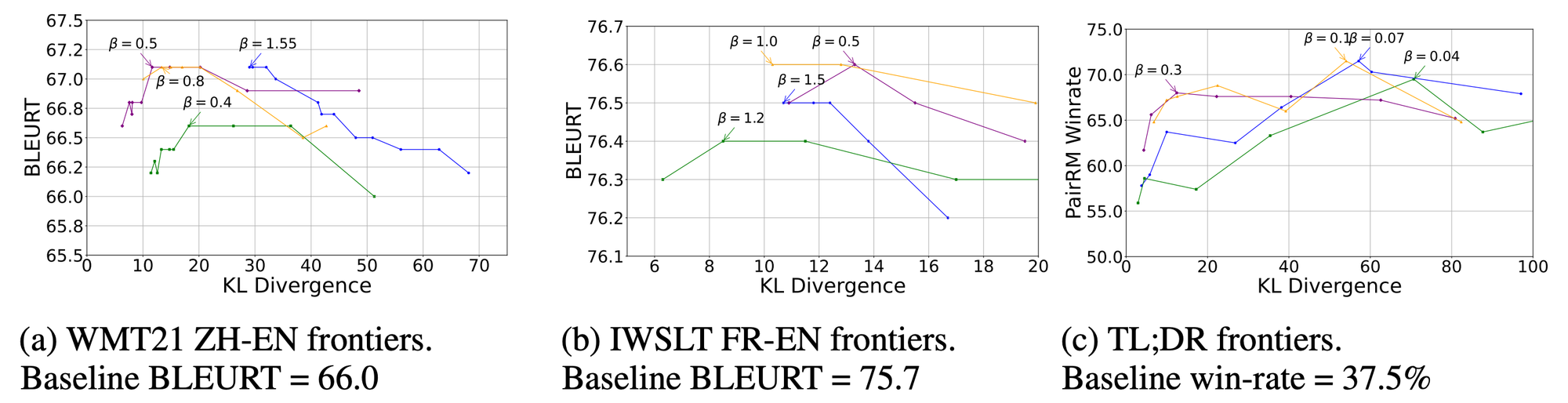
• Tied Pairs = responses ranked differently by different metrics. This often happens where multiple scoring schemes are used and we simulate the scenario on Machine Translation where several well-studied autometric metrics are available. We find that including Tied Pairs improve performance compared to simply discarding them.

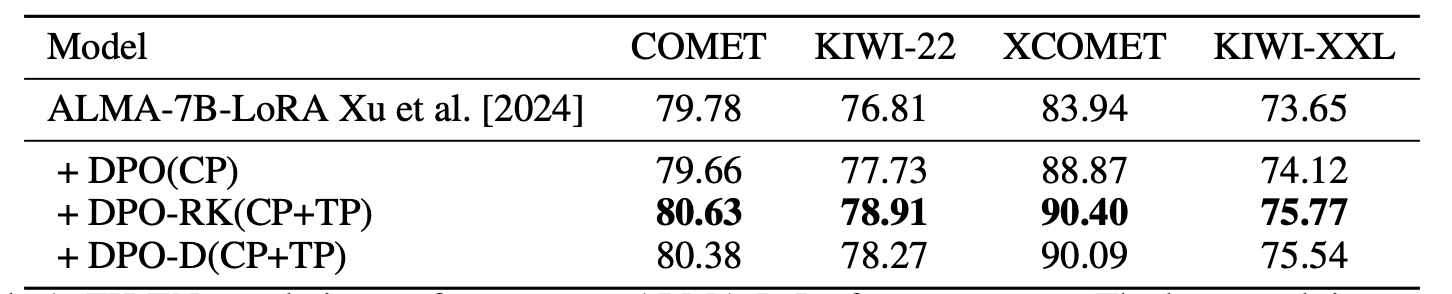
• Tied Pairs = responses that are both correct. This happens when scoring is binary, i.e., on mathematical problem solving. In sampling pairwise data from the model, we randomly choose a pair as a TP on examples where all model responses are correct. Our intuition is that since TP enhances regularization, it should contributes to maintaining behaviours on examples that the model handles well already. In our paper we further show that indeed DPO-RK(CP+TP) and DPO-D(CP+TP) better preserves correctness on questions already correctly answered by the base model.

Take-home Message

We have derived and investigated tie-compatible DPO variants. I see this work as an affirmation to Rao-Kupper's observation. Specifically, inspired by

"Any model which does not allow for the possibility of ties is not making full use of the information contained in the no-preference class."

We show that:

"DPO-RK and DPO-D can consume ties compared to DPO. Using these otherwise discarded no-preference pairs lead to stronger regularization and better task performance."

If this interests you, we invite you to read our NeurIPS 2025 paper for full derivations and experiments!