You can estimate Time-To-First-Token (TTFT), Time-Per-Output-Token (TPOT), and the VRAM (Video Random Access Memory) needed for Large Language Model (LLM) inference in a few lines of calculation. I will show you how with a real example using Llama-7B.

LLM Inference Basics

LLM inference consists of two stages: prefill and decode. In the prefill stage, the model processes the input context, computing their embeddings. In the decode stage, the model generates one token at a time conditioning on the input context and all previously generated tokens.

The speed of prefill affects Time To First Token (TTFT) as nothing can be generated before the input context is processed. Decoding speed affects Time Per Output Token (TPOT), which is the number of tokens generated per unit time after prefill. Both TTFT and TPOT are important for user experience and essential to characterizing LLM inference.

VRAM usage are dominated by model parameters and KV-cache. KV-cache is the key/value embeddings of the input context and all previous tokens. They are computed once and stored in memory to be reused in the decode stage. VRAM usage affects the maximal batch size and sequence length which can drastically affect LLM inference throughput .

To sum up, LLM inference can be characterized by VRAM usage, TTFT, and TPOT. To estimate them, we need to figure out the amount of data to load and FLOPs to compute. Let's see how.

Method

A GPU does two things: loading data and computing FLOPs. To estimate time is to estimate the total memory and compute work in each stage of LLM inference and divide by the GPU's processing rate. For that, you need the following constants:

• \(s\): sequence length
• \(b\): batch size
• \(h\): hidden dimension
• \(L\): number of transformer layers
• \(N\): model parameters
• GPU FLOPs rate. For A100, this is \(312e12\) FLOPs/second.
• GPU High Bandwidth Memory (HBM) rate. For A100, this is \(1.5\) TB/second.

We assume 16-bit precision (2 bytes per parameter), the formula are:

\[\text{Prefill Compute} = 2 \times N \times b \times s \]

\[\text{Decode Compute} = 2 \times N \times b \times 1\]

Explanation: \(2\times N\) is the approximated amount of compute needed to process each token. Consider the product \(Wx = w_{11} x_1 + w_{12} x_2 + ...\) where \(W\) is the weight matrix. Each parameter \(w_{ij}\) is involved in one multiplication (\(w_{ij} x_j\)) and one summation (\(... + w_{ij} x_j\)). \(b \times s\) is the total number of tokens to process. In the decode stage, we produce one token at a time so \(s=1\).

\[\text{Prefill Memory} = \text{Decode Memory} = 2 \times N \]

Explanation: Every model parameter needs to be loaded on to the GPU for computation. \(2\) converts model parameter count to amount of bytes assuming 16-bit precision.

Time-To-First-Token (TTFT)

\[TTFT = (\text{Prefill Compute})/(\text{FLOPs rate}) + (\text{Prefill Memory}) / (\text{HBM rate})\]

Time-Per-Output-Token (TPOT)

\[TPOT = (\text{Decode Compute})/(\text{FLOPs rate}) + (\text{Decode Memory}) / (\text{HBM rate})\]

VRAM used

\[\text{VRAM} = (\text{Model Parameters}) \times 2 + (\text{KV Cache}) \times 2 \]

\[=(\text{Model Parameters}) \times 2 + (2 \times h \times L \times b \times s )\times 2 \]

Let's interpret the KV cache expression from left two right. Each token has one cached key vector and one cached value vector in each attention head (The first \(2\)). The parameter dimension after aggregating all attention heads is the model dimension (\(\times h\)). There are (\(b \times s\)) tokens in token. The final \(\times 2\) converts parameter to bytes assuming 16-bit precision.

Llama-7B Case Study

Let's estimate TTFT and VRAM for Llama-7B inference and see if they are close to experimental values. Interpreting TPOT is highly dependent on the application context, so we only estimate TTFT in this experiment.

Here are the constants.

• \(s=256\): sequence length
• \(b=1\): batch size
• \(h=4096\): hidden dimension
• \(L=32\): number of transformer layers
• \(N=7e9\): model parameters
• GPU FLOPs rate: \(312e12\) FLOPs/second (A100-80G).
• GPU High Bandwidth Memory (HBM) rate: \(1.5\) TB/second (A100-80G).

The estimated values using the formula are:

• TTFT \(= 11.5 + 9.3 = 20.8\) ms
• TPOT \(= 0.045 + 9.3 = 9.3\) ms
• VRAM \(= 400\) MB

Estimated versus actual VRAM usage

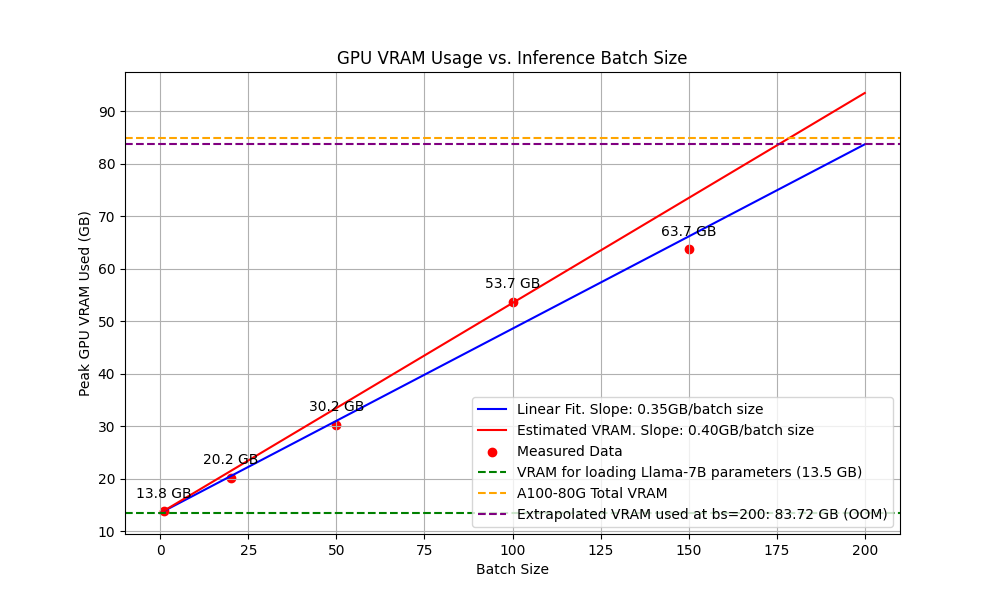
Our calculation predicts that if we plot peak VRAM used versus batch size, the slope should be close to 400MB per batch size. The linear fit to experimental data gives a slope \(=350 \text{MB/batch size}\). Our estimate is good. And as predicted, Out-Of-Memory (OOM) error is reported when batch size is set to 200.

Estimated versus actual TTFT

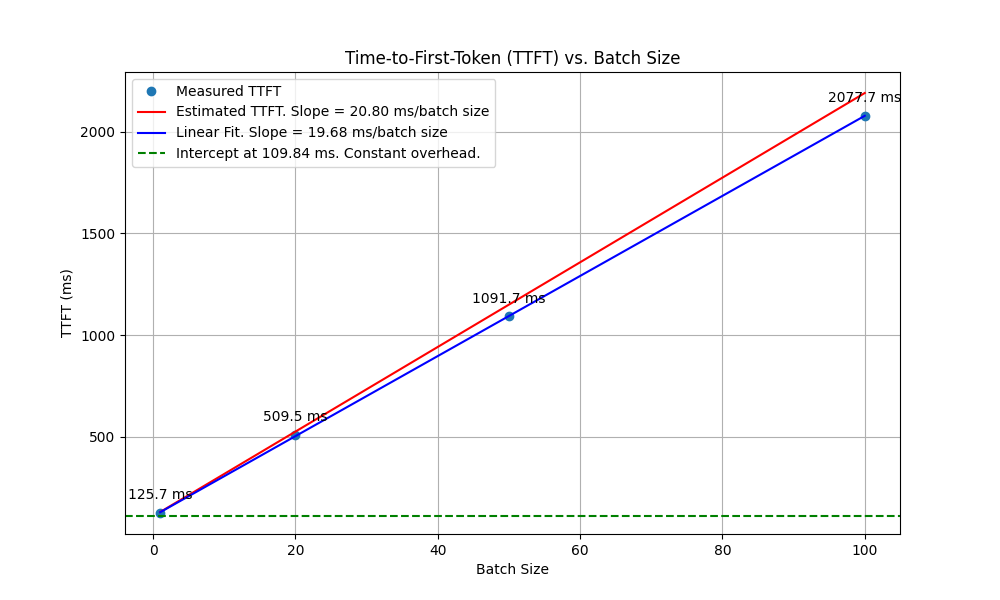
Calculation says TTFT will increase by \(20.8\) ms per batch size. We estimate TTFT by setting max_new_token=1 in huggingface .generate() call. In Figure 2, we fit a linear model on experimental TTFT versus batch size. The intercept of \(109.84\) ms reflects the constant overhead of inference. The fitted slope is \(19.68\) ms per batch size. Again, very close to our estimate of \(20.8\)!

Conclusion

Simple calculation gives TTFT and VRAM estimates close to experimental results. You can use it to estimate LLM inference speed, maximal batch size, and whether you need a GPU with more VRAM. Experiment code provided on request.

I will cover speed and VRAM for training in another post.

The method is shared in a talk by Linden Li @NeurIPS 2023. Slides: https://linden-li.github.io/posts/inference-slides.