[538 words, 2-minute read]

A family of lossless LLM inference acceleration techniques has been developed based on speculative sampling (review here). Proposed by Google and Deepmind, speculative sampling is the following three-step procedure:

1. Draft: a small model (draft model, \(p(\cdot|\text{context})\)) quickly generates a K-token draft.
2. Verify: the big LLM (target model, \(q(\cdot|\text{context}+\text{draft})\)) evaluates the draft with one forward pass.
3. Accept/Resample: Decide the longest prefix in the draft to accept and sample a token from an adjusted distribution, \(\text{normalize}(\max(0, q(x)-p(x)))\), to replace the first rejected token. Repeat.

This post explains how you can derive the "Accept/Resample" step from an intuitive example.

Formal Accept/Resample Rule

Given a distribution \(q\) from which we wish to sample and a proxy distribution \(p\), the speculative sampling accept/resample rule guarantees that the samples follow \(q\) even when we are drawing samples from \(p\):

• Draw sample \(\tilde x \sim p\). If \(q(\tilde x) > p(\tilde x)\), accept the sample (\( x = \tilde x\)).
• Otherwise, draw a new sample from the adjusted distribution \((q(x) - p(x))_{+}\), where \(f(x)_{+}\) denotes \(\frac{\max(0, f(x)}{\sum_x \max(0, f(x))}\), which is a normalized probability mass difference.

The proof from DeepMind's paper is simple but gives little insight into how the method was first discovered. Let's rediscover the resample rule with a simplified example.

Rediscovering the Resample Rule

Let \(x\) be a binary random variable that takes the value of either \(0\) or \(1\). Let \(q(x) = (0.3, 0.7)\) and the proposal distribution \(p(x) = (0.5, 0.5)\). Figure 1 illustrates the probability mass function (pmf) of \(q\) and \(p\).

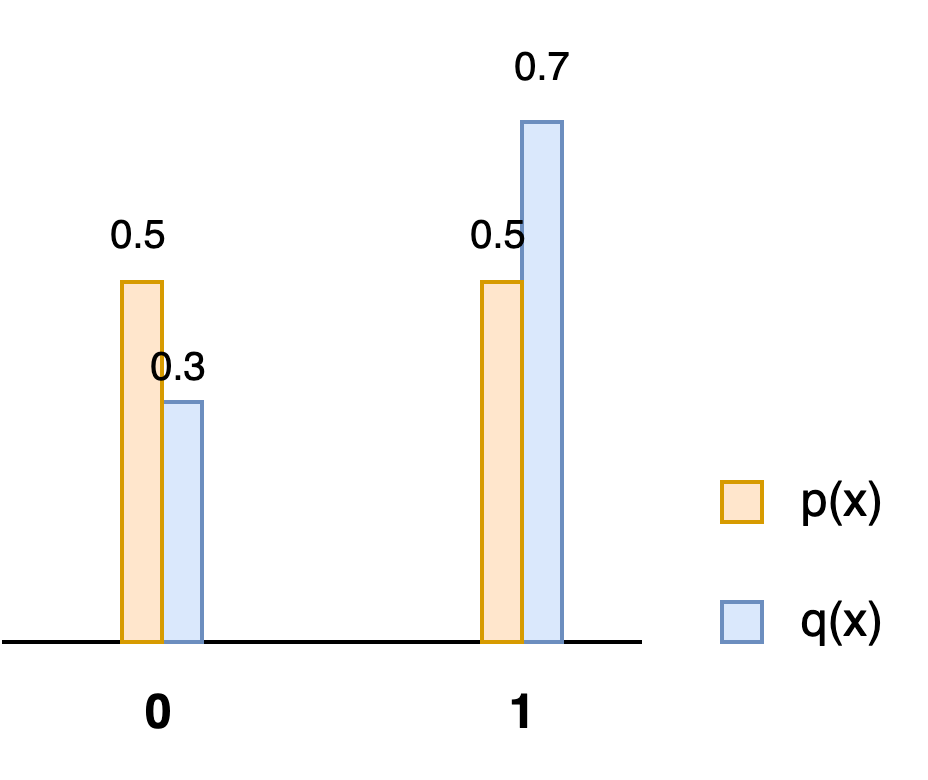
Now consider the speculative sampling procedure: if the proposal is \(\tilde x = 1\), the sample will always be accepted. This means the \(pmf(x = 1)\) gains a probability mass of \(0.5\). However, the true probability mass is \(0.7\), This means the accept/resample rule must retrain \(0.3\) of the probability mass from \(pmf(\tilde x=0)\) to form \(pmf(x=0)\) and transfer \(0.2\) to probability mass \(pmf(x=1)\). To do this:

• when \(\tilde x=0\) is proposed, we accept it with probability\(\frac{0.3}{0.5} = 0.6\). This leaves \(pmf(x=0) = 0.5\times 0.6 = 0.3\) .
• If \(\tilde x=0\) is rejected, we resample \(x=1\) so that \(0.4\times 0.5 = 0.2\) probability mass is moved to \(pmf(x=1)\). Overall, \(pmf(x)\) is exactly as \(q(x)=(0.3, 0.7)\).

It is straight-forward that in the multi-variate case, we should resample according to the difference in probability mass between the target and the proxy distribution, which is the adjusted distribution \((q(x) - p(x))_{+}\) in the formal definition.

Conclusion

The example makes clear that accept and resample in speculative decoding correspond to retaining and transferring probability mass from the proposal distribution, respectively. Speculative sampling is the foundation of an array of more advanced LLM inference acceleration methods. You can find a short review here.