Data Contribution Estimation (DCE) for Machine Learning: Tutorial@NeurIPS 2023 in 10-minutes

Prof. Ruoxi Jia, the tutorial's presentor has kindly proofread this summary.

Data Contribution Estimation (DCE) estimates how important a training data point is to the model's performance. People use DCE to (1) find mislabeled data that has negative impact on performance; (2) conduct data valuation to reward or compensate data providers with fair monetary values; and (3) identify memorized information to tackle privacy issues. This tutorial reviews the classes of DCE methods and its application to Large Language Models (LLMs). This post summarizes it in 700 words.

Valuate data points with LOO, Shapley value, and Banzhaf value

The importance of a data point can be measured by how much the model performance degrades if that data point is removed from the training set. We can compute the Leave-One-Out (LOO) error for a specific data unit \(d\) with the following steps: train the model on the training dataset, evaluate on the validation set, train another model but excluding the data point of interest in training, and compute the performance difference.

\[LOO(d) =\text{Score(train_data}) - \text{Score(train_data } - \text{ unit } d\text{)}\]

LOO only measures degradation with one pair of evaluations and the training process is stochastic. This makes LOO susceptible to noise and high variability. The Shapley value remedies this by taking a weighted average of LOO over all possible subsets of the training data. The weights are inversely proportional to the number of subsets of a given dataset cardinality, preventing medium-sized subsets from dominating. There are strong empirical evidence that Shapley value is more informative than LOO.

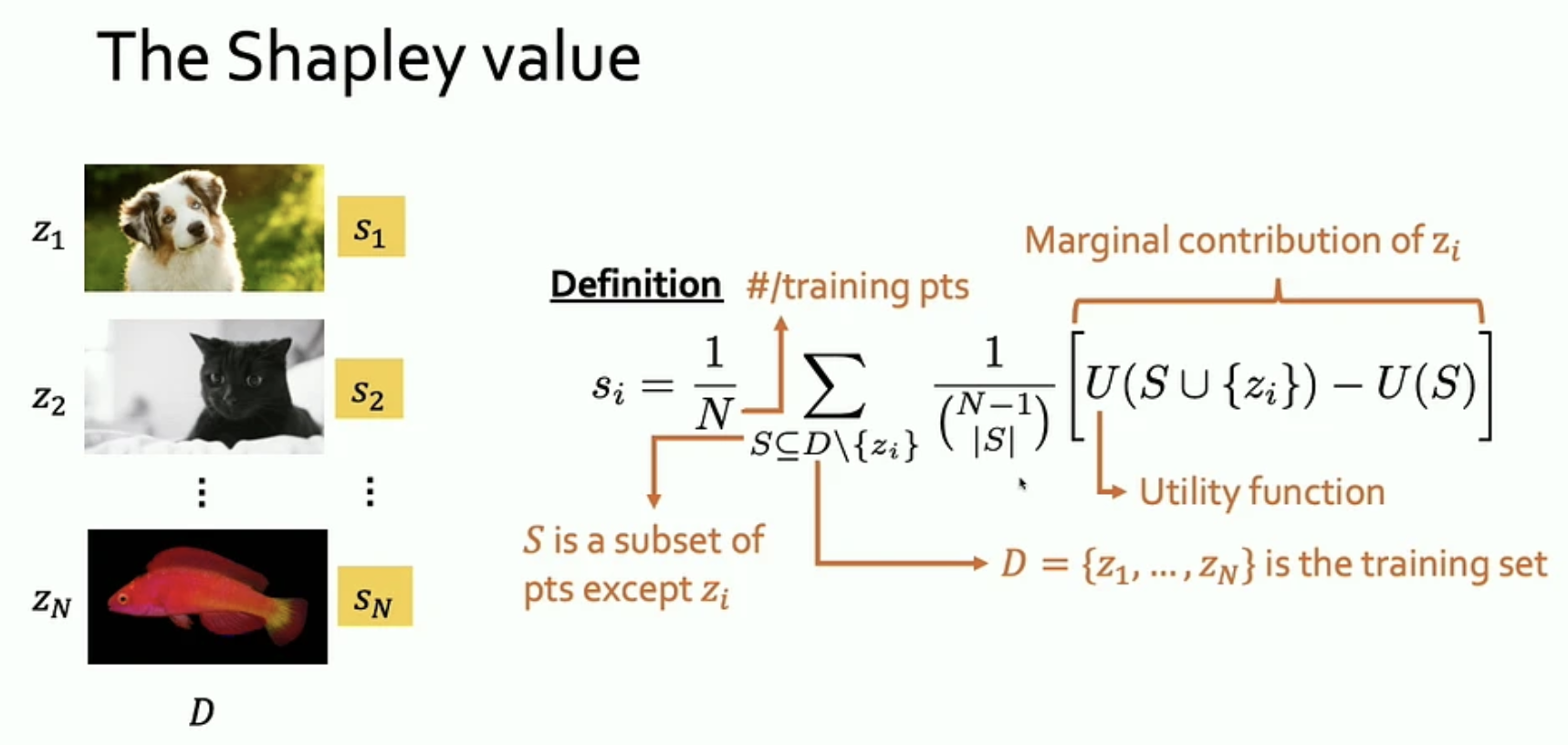
The Shapley value is originally proposed in cooperative game theory by Lloyd Shapley, 2012 Nobel laureate in Economics. The Banzhaf value is the unweighted version of the Shapley value. Both have been applied in DCE as importance of data point. The Shapley value has the nice property that the total value is fully distributed among individual data points (known as "Efficiency"), whereas the Banzhaf value is more robust in preserving rankings among data points when the utility function is perturbed (Safety Margin).

Computationally tractable DCE methods​

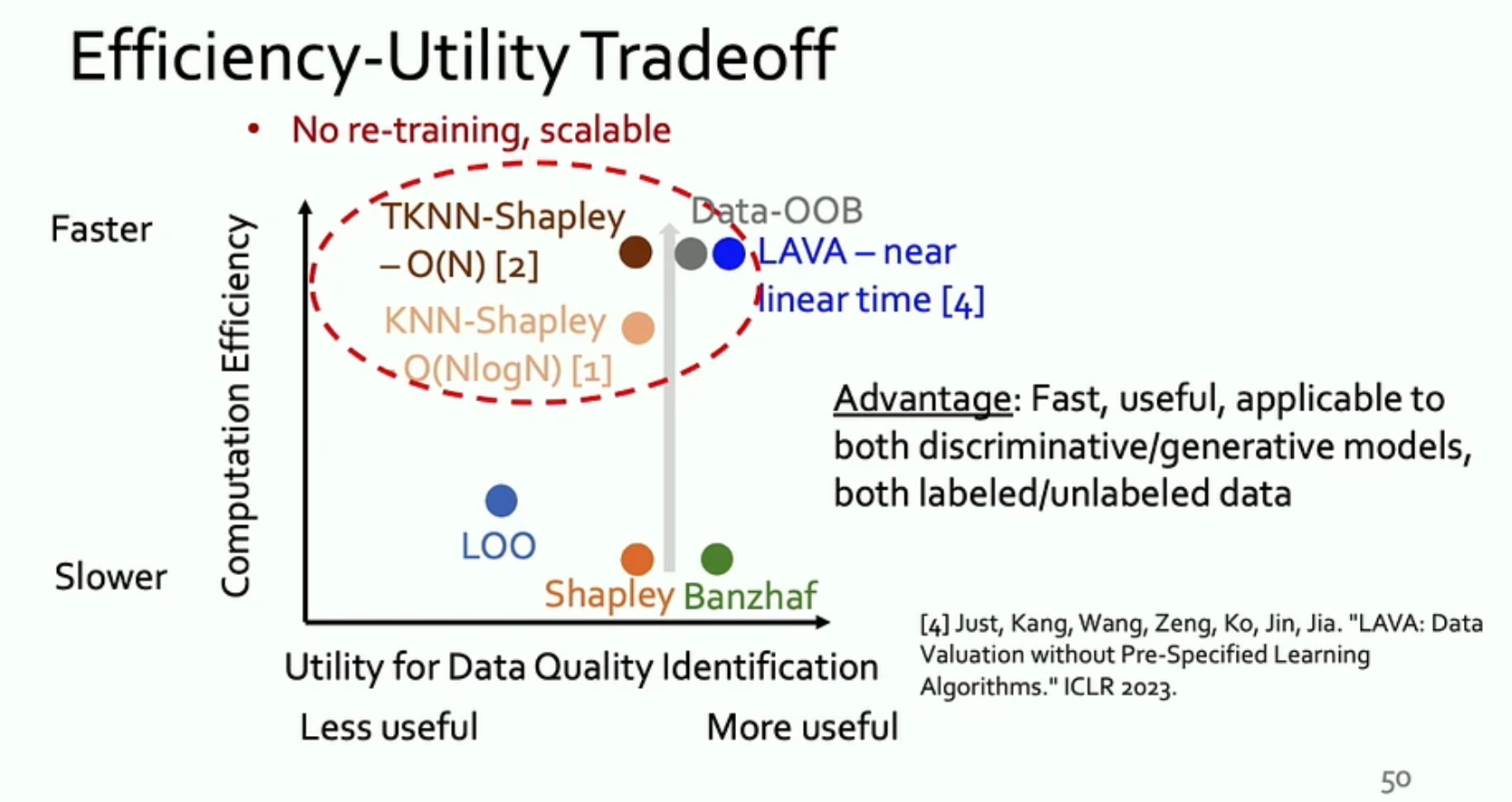
Training modern neural models and evaluate on every dataset permutation is clearly intractable. There are three major approaches to make computing Shapley value tractable:

1. Monte Carlo Estimation: compute Shapley over a sampled set of permutations instead of all permutations. Truncated Monte Carlo stops scanning over the data points in a permutation when the score difference is small enough.
2. K-Nearest-Neighbor approximation: for neural models, this means using a KNN majority voting classifer on the final learned embedding space. This saves compute in two ways: (a) only one training run is required to obtain the embedding space; (b) data points other than the K-nearest neighbors have no effect on the KNN classification result, hence can have zero contribution to many subsets. This allows us to tractably compute the exact Shapley value in the locality. KNN-Shapley achieves \(O(N\log N)\) whereas TKNN-Shapley published in NeurIPS 2023 achieves \(O(N)\) complexity.
3. Approximate validation performance with distributional distance: instead of training a model to evaluate its performance on the validation set, use the distributional distance between the training and validation set as a proxy of model performance. Intuitively, a zero distributional distance means the training set is identically distributed as the test set. Therefore, a model well-trained on the training set should perform well on the validation set. Distributional distance can be evaluated by Optimal Transport (OT). LAVA implements this idea where no model training is required.

Here's a summary of how these methods stand in usefulness and efficiency.

Applications to Large Language Models (LLMs)

DCE can be used to (1) curate higher-quality data. The LIMA paper shows fine-tunig on higher-quality data in smaller quantity is better than on lots of low-quality data. (2) understand and better select better in-context learning examples, drawing on insights from What Makes In-Context Learning Work?.

Conclusion & Future Direction

There are computationally tractable DCE methods based on KNN simplification and distributional distance. In my view, applying DCE to LLMs awaits further investigations. Feasibility to compute Shapley value at large scale and extending KNN-based Shapley value computation to generative model remain two active research questions.

Let me know in the comments if you find the summary helpful!